Dynamics and Markov Analysis

Dynamics

Levels of pLQ can be considered as levels of LQ corrected by size effects. This section explores the persistence of pLQ levels through a Markovian transitions analysis. It reveals that pLQ levels near 0 and 1 are stable, while transitions between these extremes often involve intermediate values.

Figure 1 below illustrates the relationship between $pLQ_t$ (horizontal axis) and $pLQ_{t+1}$ (vertical axis), resembling an empirical Markov matrix. Key observations include:

• Stability: Very low and high pLQ levels tend to remain stable over time.
• Volatility: Intermediate pLQ levels exhibit higher volatility, with significant chances of varying outcomes over time.

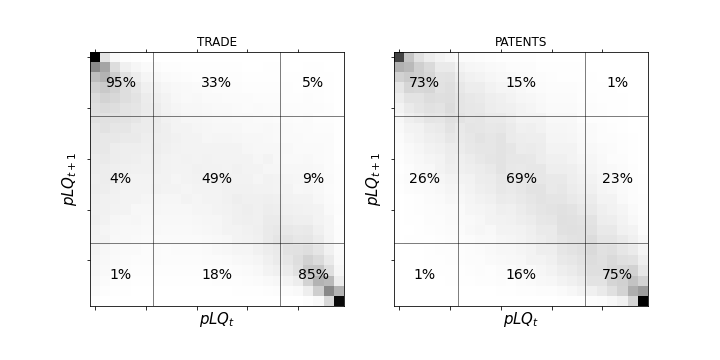
Figure 1: Plot of an empirical Markov matrix showing pLQ next year as a function of pLQ this year. Both extremes show persistence, while the values in the middle show high volatility. The gray intensity denotes percentage probability in the Markov cell, from 0% (white) to 100% (black).

Categorizing pLQ Levels

By partitioning pLQ into three categories, we can derive further insights:

• Low values: $0 < \text{pLQ} < 0.25$
• Medium or transition values: $0.25 < \text{pLQ} < 0.75$
• High values: $0.75 < \text{pLQ} < 1$

This categorization allows the computation of a $3 \times 3$ Markov matrix, revealing:

• Significant probabilities of transitions between categories 1 and 2, and between categories 2 and 3.
• Reduced probabilities of direct transitions between categories 1 and 3 without passing through 2.

This suggests an ordering in LQ values, where the transition category acts as a stage for country-products moving between no-advantage and advantage statuses.

Implications for Network Analysis

Studies using $LQ > 1$ for defining binary matrices and bipartite networks can leverage pLQ for a weighted bipartite network. This Markov analysis confirms that pLQ levels can define categorical values {low, mid, high} instead of binary {0, 1} values.