Micro to Macro Fluctuations
Understanding the Transition from Micro to Macro Fluctuations
This section provides an overview of how micro-level fluctuations aggregate into macro-level fluctuations, both in linear and log terms. The scheme in Figure 1 illustrates the relationships and equations discussed below.
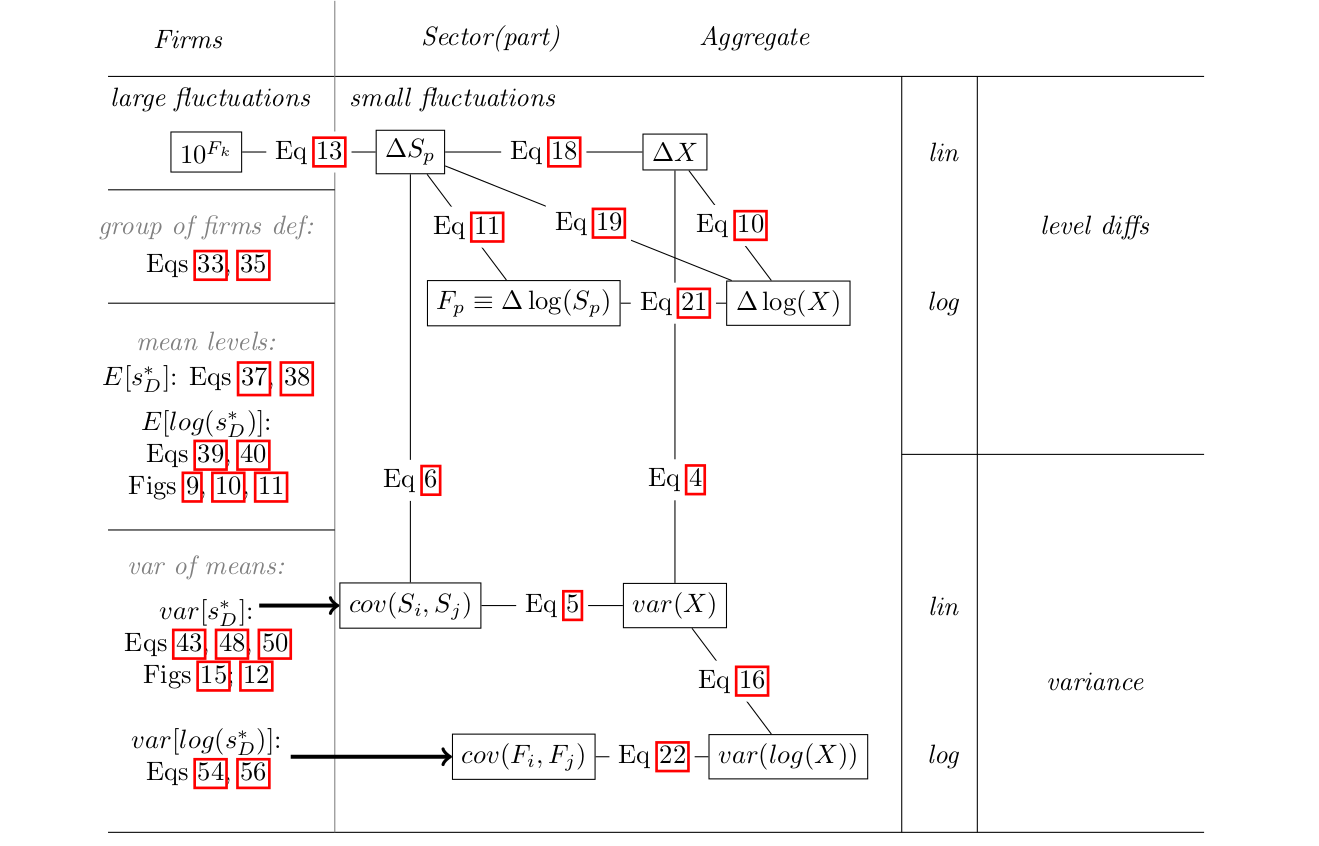
Key Components
-
Firms:
- Large fluctuations are represented by .
- Group of firms defined by specific equations:
- Quantile Sum: Refer to Eq quantile_sum.
- Power Sum: Refer to Eq power_sum__narrow_bin.
- Mean levels:
- : See Eqs E_N, E_L.
- : See Eqs Elog_N, Elog_L and Figures Elog_mu0_fnq_0, Elog_sigma0_fmu_0, Elog_mu0_fsigma_0.
- Variance of means:
- : See Eqs alpha_1, var_N, var_L and Figures var_mu0_fsigma_0, fig:var_mu0_fnq_0.
- : See Eqs var_log_N, var_log_L.
-
Sector and Aggregate:
- Level differences:
- and .
- Equations: to (Eq eqa), to (Eq Ft_def).
- Variance:
- and .
- Equations: to (Eq var_cov_sum_def), to (Eq var_log_shocks).
- Level differences:
Equations and Relationships
- Growth Rate Equation:
- to (Eq growth_rates).
- Variance in Terms of Deltas:
- to (Eq var_delta).
- Logarithmic Relationships:
- to (Eq parts_linear_approx).
- to (Eq var_log).
This structured approach helps in understanding how individual firm-level fluctuations can aggregate into sectoral or macroeconomic fluctuations, emphasizing the importance of both linear and logarithmic transformations.